
SEBA Class 9th To 12th Syllabus 2023- Physics, Chemistry, Maths & Biology (Science Stream)
SEBA Syllabus 2023: The Secondary Education Board of Assam (SEBA) has published the Class 9th and 10th syllabus 2023-24 academics on the official site at sebaonline.org and Higher Secondary Class 11th and 12th on the official site at ahsec.assam.gov.in.
Check out the SEBA class 9th to 12th Syllabus 2023-24 in this article to help you enhance your academic result in this session for Science subjects (Physics, Chemistry, Mathematics & Biology)
Class 9th Syllabus 2023-24
This year, you will witness a more specialized and in-depth approach to subjects. Discover the fascinating world of Physics, Chemistry, and Biology, while Mathematics becomes more analytical.
General Mathematics- Code C2 (Total -100 Marks)
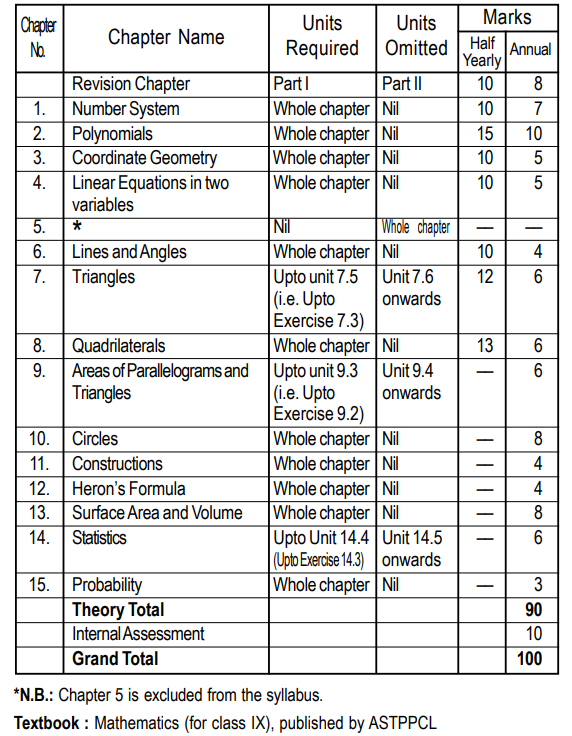
Unit 1: Number Systems
*Real numbers:
Review of representation of natural number, integers, rational numbers on the number line. Representation of terminating/non-terminating recurring decimals, on the number line through successive magnification. Rational numbers as recurring/terminating decimals. Examples of non-recurring/non-terminating decimals such as 2, 3, 5 etc. Existence of non-rational numbers (irrational numbers) such as 2, 3 and their representation on the number line. Explaining that every real number is represented by a unique point on the number line, and conversely, every point on the number line represents a unique real number.
Existence of x for a given positive real number x (visual proof to be emphasized). Definition of nth root of real number.
Recall of laws of exponents with integral powers.
Rational exponents with positive real bases (to be done by particular cases, allowing learner to arrive at the general laws.)
Rationalisation (with precise meaning) of real number of the type (and their combinations)
where x and y are natural numbers and a, b are integers.
Unit 2: Algebra
*Polynomials
Definition of a polynomial in one variable, its coefficients, with examples and counter examples, its terms, zero polyonimal. Degree of a polynomial. constant, linear, quadratic, cubic polynomials; monomials, binomials, trinomials. Factors and multiples. Zeros/roots of a
polynomial/equation. State and motivate the ‘Remainder Theorem with examples and analogy to integers. Statement and proof of the Factor Theorem.
Factorisation of () where a,b, c are real numbers, and of cubic polynomials using the Factor Theorem.
*Co-ordinate Geometry
The Cartesian plane, coordinates of a point, names and terms associated with the coordinate plane, notations, plotting points in the plane, graph of linear equations as examples; focus on linear equations of the type ax by c 0by writing it as y mx c and linking with the chapter on linear equations in two variables,
*Linear Equations in Two Variables
Recall of linear equations in one variable. Introduction to the equation in two variables. Prove that a linear equation in two variables has infinitely many solutions, and justify their being written as ordered pairs of real numbers, plotting them and showing that they seem to lie on a
line. Examples, problems from real life, including problems on Ratio and Proportion and with algebraic and graphical solutions being done simultaneously.
Unit 3: Geometry
*.Introduction to Euclid’s Geometry
History-Euclid and geometry in India. Euclid’s method of formalizing observed phenomenon into rigorous mathematics with definitions, common/obvious notions,
axioms/postulates and theorems. The five postulates of Euclid. Equivalent versions of the fifth postualate.
Showing the relationship between axiom and theorem.
1. Given two distinct points, there exists one and one
only one line through them.
2. (Prove) Two distinct lines cannot have more than
one point in common.
*.Lines and Angles
i) (Motivate) If a ray stands on a line, then the sum of the two adjacent angles so formed is 1800 and the converse.
ii) (Prove) If two lines intersect, the vertically opposite angles are equal.
iii) (Motivate) Results on corresponding angles, alternate angles, interior angles when a transversal intersects two parallel lines.
iv) (Motivate) Lines, which are parallel to a given line, are parallel.
v) (Prove) The sum of the angles of a triangle is 1800
vi) (Motivate) If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two remote interior angles.
*.Triangles
i) (Motivate) Two triangles are congruent if any two sides and the included angle of one triangle is equal to any two sides and the included angle of the other triangle (SAS Congruence).
ii) (Prove) Two triangles are congruent if any two angles and the included side of one triangle is equal to any two angles and the included side of the other triangle (ASA Congruence).
iii) (Motivate) Two triangles are congruent if the three sides of one triangle are equal to three sides of the other triangle (SSS Congruence)
iv) (Motivate) Two right triangles are congruent if the hypotenuse and a side of one triangle are equal (respectively) to the hypotenuse and a side of the other triangle.
v) (Prove) The angles opposite to equal sides of a triangle are equal.
vi) (Motivate) The sides opposite to equal angles of a triangle are equal.
vii) (Motivate) Triangle inequalities and relation between ‘angle and facing side; inequalities in a triangle.
*.Quadrilaterals
i) (Prove) The diagonal divides a parallelogram into two congruent triangles.
ii) (Motivate) In a parallelogram opposite angles are equal and conversely.
iii) (Motivate) In a parallelogram opposite sides are equal and conversely.
iv) (Motivate) A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and equal.
v) (Motivate) In a parallelogram, the diagonals bisect each other and conversely.
vi) (Motivate) In a triangle, the line segment joining the
mid points of any two sides is parallel to the third side and (motivate) its converse.
*.Area
Review concept of area, recall area of a rectangle.
i) (Prove) Parallelograms on the same base and between the same parallels have the same area.
ii) (Motivate) Triangles on the same base and between the same parallels are equal in area and its converse.
*.Circle
Through examples, arrive at definitions of circle. related
concepts, radius, circumference, diameter, chord, arc, subtended angle.
i) (Prove) Equal chords of a circle subtend equal angles at the centre and (motivate) its converse.
ii) (Motivate) The perpendicular from the centre of a circle to a chord bisects the chord and conversely, the line drawn through the centre of a circle to bisect
a chold is perpendicular to the chord.
iii) (Motivate) There is one and only one circle passing through three given non-collinear points.
iv) (Motivate) Equal chords of a circle (or of congruent circles) are equidistant from the centre (s) and conversely.
v) (Prove) The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
vi) (Motivate) Angles in the same segment of a circle are equal.
vii) (Motivate) If a line segment joining two points subtends equal angle at two different points lying on the same side of the line containing the segment, the four points lie on a circle.
viii)(Motivate) The sum of the either pair of the opposite angles of a cyclic quadrilateral is 1800 and its converse.
*.Constructions
i) Construction of bisectors of a line segment and angle, 60Degree, 90Degree , 45Degree etc, equilateral triangles.
ii) Construction of a triangle given its base, sum/ difference of the other two sides and one base angle.
iii) Construction of a triangle of given perimeter and base angles.
Unit 4: Mensuration
*.Area
i) Surface Areas and Volumes : Area of a triangles using Heron’s formula (without proof) and its application in finding the area of a quarilateral.
ii) Surface Areas and Volumes : Surface areas and volumes of cubes, cuboids,
spheres (including hemispheres) and right circular cylinders/cones.
Unit 5: Statistics and Probability
*.Statistics
Introduction to Statistics : Collection of data, Presentation of data-tabular form, ungrouped/grouped, frequency polygons, qualitative analysis of data to choose the correct form of presentation for the correct data. Mean median, mode of ungrouped data.
*.Probability
History, Repeated experiments and observed frequency approach to probability. Focus is on empirical probability. (A long period of time to be
devoted to group and to individual activities to motivate the concept; the experiments to be drawn from real-life situations, and from examples used in the chapter on statistics).
General Science- Code C3 (Total -100 Marks)
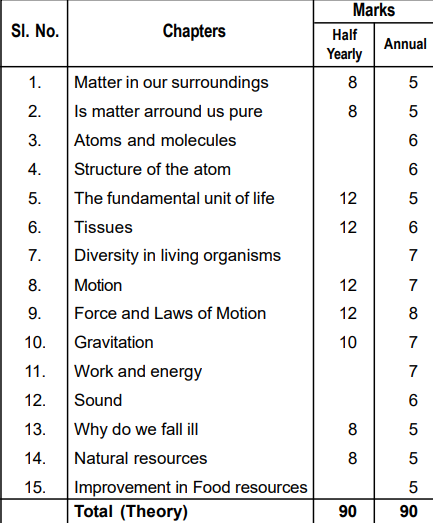
Unit1: Matter in Our Surroundings
Unit 2: Is Matter Around Us Pure
Unit 3: Atoms and Molecules
Unit 4: Structure of Atoms
Unit 5: The Fundamental Unit Of life
Unit 6: Tissues
Unit 7: Diversity of Living Organisms
Unit 8: Motion
Unit 9: Force and Laws of Motion
Unit 10: Gravitation
Unit 11: Work and Energy
Unit 12: Sound
Unit 13: Why Do We Fall ill
Unit 14: Natural Resources
Unit 15: Improvement In Food Resources
Advanced Mathematics- Code 19 (Total -100 Marks)
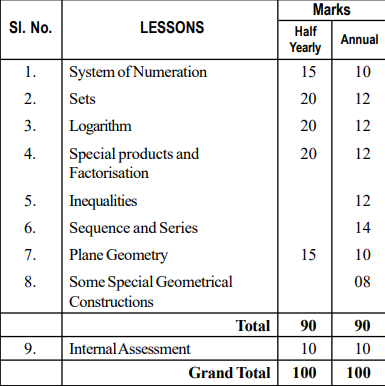
Unit-1. Set
Algebra of sets :
Proofs of laws of Algebra of sets. Derivation of n(A∪ B)=
n (A) + n (B) – n (A ∩ B). Relation as subset of Cartesian
product, function. Concepts of reflexive, symmetric and transitive relation. Equivalence relation.
Unit 2 : Complex Number :
1. Introduction to imaginary numbers.
2. Complex number, as an ordered pair of real numbers.
3. Operations of complex numbers.
4. Properties of complex numbers.
5. Diagramatic representation of a complex number in a plane.
6. Conjugate complex number, properties of conjugate complex numbers.
7. Modulus of complex number and properties.
8. Argument of a complex number and properties.
9. Representation of complex number in (r, θ) form
10. In a quadratic equation, complex roots occur in conjugate pair (without proof).
11. Square root of complex number.
Unit -3 : Arithmetic of integers :
Method of induction (Statement only) and simple applications. Divisibility of Integers : Division algorithm,
Greatest Common Divisor (GCD), simple properties of GCD.
If d is the GCD of two integers a and b then there exist integers x and y such that d = ax+by.
Least common multiple (LCM) of integers. Theorem on
GCD & LCM, Calculation of GCD of two integers by Euclid’s Algorithm. Prime numbers, composite numbers
perfect number, reletive prime nos. congruence of integers modulo, properties of modular congruence.
Unit – 4 : Quadratic equation :
Formation of quadratic equation from roots, equations reducible to Quadratic equation. Application problems involving quadratic equation. Simultaneous equations in two variables – one linear and other quadratic.
Unit – 5 : Application of Common Logarithm :
Characteristic and Mantissa. Use of Log table in numerical calculations.
Unit -6 : Permutation & Combination :
Combination and Permutation of distinct objects only.
Symbols n Cr and n Pr with proofs. Restricted permutations and combinations, applications in simple problems.
Unit -7 : Plane Trigonometry :
Trigonometric ratios for
angles θ, 900 ± θ, 1800 ± θ,2700 ± θ, 3600 ± θ.
Trigonometric ratios of compound angles : Formula for sin (A ± B), cos (A ± B), tan (A ± B), (Idea of multiple angles and with simple application excluding identities)
Unit -8 : Plane Geometry :
Proofs of the following theorems and exercises on them :
(i) The angles made by a tangent to a circle with a chord drawn from point of contact are respectively equal to the angles in the alternate segments of the circle.
(ii) If two chords of a circle cut at a point within or outside it, the rectangles contained by their segments are equal.
(iii) If a straight line drawn from an external point P intersects a circle at A and B and a straight line drawn from P touches the circle at T then PA. PB = PT2.
(iv) The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle. (The corresponding theorem about an external
bisector should be given as an exercise).
(v) If the vertical angle of a triangle is bisected by a straight line which cuts the base, the rectangle contained by the sides of the triangle is equal to the rectangle contained by the segment of the base, together with the square on the straight line which bisects the angle.
(vi) The rectangle contained by the diagonals of a quadrilateral inscribed in a circle is equal to the sum of the two rectangles contained by the opposite sides.
Unit -9 : Co-ordinate Geometry : Straight line :
Every first degree equation in x and y represents a straight
line. Equation of straight line in gradient form, intercept form and normal form, passing through two points. Angle between two straight lines and condition of perpendicularity and parallelism.
Class 10th Syllabus 2023-24
This year, you will witness a more specialized and in-depth approach to subjects. Discover the fascinating world of Physics, Chemistry, and Biology, while Mathematics becomes more analytical.
General Mathematics- Code C2 (Total -100 Marks)

Unit I. Number Systems
Real Numbers
Euclid’s division lemma, Fundamental Theorem of Arithmetic-statements after reveiwing work done earlier and after illustrating and motivating through examples. Proofs of results-irrationality of √2, √3, √5, decimal expansions of
rational numbers in terms of terminating/non-terminating recurring decimals.
Unit II. Algebra
1. Polynomials
Zeros of a polyomial. Relationship between zeros and coefficients of a polynomial with particular reference to quadratic polynomials. Statement and simple problems on division algorithm for polynomials with real coefficients.
2. Pair of Liner Equations in Two Variables
Pair of linear equations in two variables. Geometric representation of different possibilities of solutions/ inconsistency.
Algebraic conditions for number of solutions. Solution of pair of linear equations in two variables algebraically-by substitution, by elimination and by cross multiplication. Simple situational problems must be included. Simple problems on equations reducible to linear equations may be included.
3. Quadratic Equations
Standard form of a quadratic equation ax2 + bx + c = 0, (a ¹ 0). Solution of quadratic equations (only real roots)by factorization and by completing the square, i.e. by using quadratic formula. Relationship between
discriminant and nature of roots. Problems related to day-to-day activities to be
incorporated.
4. Arithmetic Progressions (AP)
Motivation for studying A.P. Derivation of standard results of finding the nth terms and sum of first n terms.
Unit III : Trigonometry
1. Introduction to Trigonometry
Trigonometric ratios of an acute angle of a right-angled triangle. Proof of their existence (well defined); motivate the ratios, whichever are defined at 0degree
and 90degree. Values (with proof) of the trigonometric ratios of 30degree
, 45degree and 60degree. Relationship between the ratios.
Trigonometric Identities : Proof and applications of
the identity sin2 A + cos2 A=1, sec2 A – tan2 A=1, cosec2 A – cot2A = 1. Only simple identities to be given. Trigonometric ratios of complementary angles.
2. Heights and Distances (Not from examination point of view)
Simple and believable problems on heights and distances. Problems should not involve more than two right triangles. Angles of elevation/depression should be only 30degree, 45degree, 60degree
Unit IV : Coordinate Geometry
Lines (In two-dimensions)
Review the concepts of coordinate geometry done earlier including graphs of linear equations. Awareness of geometrical representation of quadratic polynomials. Distance between two points and section formula (internal). Area of a triangle.
Unit V : Geometry
1. Triangles
Definitions, examples, counter examples of similar
triangles.
i) (Prove) If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
ii) (Motivate) If a line divides two sides of a triangle in the same ratio, the line is parallel to the third side.
iii) (Motivate) If in two triangles, the corresponding angles are equal, their corresponding sides are proportional and the triangles are similar.
iv) (Motivate) If the corresponding sides of two triangles are proportional, their corresponding angles are equal and two triangles are similar.
v) (Motivate) If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional, the two triangles are similar.
vi) (Motivate) If a perpendicular is drawn from the vertex of the right angle to the hypotenuse, the triangles on each side of the perpendicular are similar to the whole triangle and to each other.
vii) (Prove) The ratio of the areas of two similar triangles is equal to the ratio of the squares on their corresponding sides.
viii) (Prove) In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
ix) (Prove) In a triangle, if the square of one side is equal to sum of the squares of the other two sides, the angle opposite to the first side is a right triangle.
2. Circle
Tangent to a circle at any point on it is motivated by chords drawn from points coming closer and closer to the point.
i) (Prove) The tangent at any point of a circle is perpendicular to the radius through the point of contact.
ii) (Prove) The lengths of tangents drawn from an external point to a circle are equal.
3. Constructions
i) Division of a line segment in a given ratio (internally).
ii) Tangent to a circle from a point outside it.
iii) Construction of a triangle similar to a given triangle.
Unit : VI. Mensuration :
1. Areas Related to Circles
Motivate the area of a circle; area of sectors and segments of a circle. Problems based on areas and perimeter/circumference of the above said plane figures.
(In calculating area of segment of a circle, problems should be restricted to central angle of 60degree, 90degree, and 120degree only. Plane figures involving triangles, simple quadrilaterals and circle should be taken.)
2. Surface Areas and Volumes
i) Problems on finding surface areas and volumes of combinations of any two of the following: cubes, cuboids, spheres, hemispheres and right circular cylinders/cones. Frustum of a cone.
ii) Problems involving converting one type of metalic solid into another and other mixed problems. (Problems with combination of not more than two different solids be taken.)
Unit : VII. Statistics and Probability
1. Statistics
Mean, median and mode of grouped data (bimodal situation to be avoided).
Cumulative frequency graph.
2. Probability
Classical definition of probability. Connection with probability as given in Class IX. Simple problems on single events, not using set notation.
General Science- Code C3 (Total -100 Marks)

Class 11th Syllabus 2023-24 (Science Stream)
The final two years of secondary education open up new avenues for academic growth. Class 11 and 12 offer you the flexibility to choose subjects according to your interests and aspirations. Whether it’s Science, Commerce, or Arts, SEBA empowers you with a wide array of options. Dive deep into your chosen subjects, broaden your intellectual horizons, and get ready to take on the world beyond the classroom.
Physics (70 Marks)

Unit I: Physical World and Measurement.
Chapter–1: Physical World
Chapter–2: Units and Measurements Need for measurement: Units of measurement; systems of units; SI units, fundamental and derived units. significant figures. Dimensions of physical quantities, dimensional analysis
and its applications.
Unit II: Kinematics
Chapter–3: Motion in a Straight Line
Elementary concepts of differentiation and integration for describing motion, uniform and non- uniform motion, Frame of reference and instantaneous velocity, uniformly accelerated motion, velocity – time and position-time graphs.
Relations for uniformly accelerated motion (graphical treatment).
Chapter–4: Motion in a Plane
Scalar and vector quantities; position and displacement vectors, general vectors and their notations; equality of vectors, multiplication of vectors by a real number, addition and subtraction of vectors, Unit vector; resolution of a vector in a plane, rectangular components, Scalar and Vector product of vectors. Motion in a plane, cases of uniform velocity and uniform acceleration- projectile motion, uniform circular motion.
Unit III: Laws of Motion
Chapter–5: Laws of Motion
Intuitive concept of force, Inertia, Newton’s first law of motion; momentum and
Newton’s second law of motion; impulse; Newton’s third law of motion.
Law of conservation of linear momentum and its applications.
Equilibrium of concurrent forces, Static and kinetic friction, laws of friction, rolling friction, lubrication. Dynamics of uniform circular motion: Centripetal force, examples of circular motion (vehicle on a level circular road, vehicle on a banked road). Solving problem in mechanics.
Unit IV: Work, Energy and Power
Chapter–6: Work, Energy and Power
Work done by a constant force and a variable force; kinetic energy, work- energy theorem, power. Notion of potential energy, potential energy of a spring, conservative forces: conservation of mechanical energy (kinetic and potential energies); nonconservative forces: motion in a vertical circle; elastic and inelastic collisions in one and two dimensions.
Unit V: Motion of System of Particles and Rigid Body.
Chapter–7: System of Particles and Rotational Motion
Centre of mass of a two-particle system, momentum conservation and motion of centre of Mass, Centre of mass of a rigid body; centre of mass of a uniform rod. Moment of a force, torque, angular momentum, law of conservation of angular momentum and its applications.
Equilibrium of rigid bodies, rigid body rotation and equations of rotational motion, comparison of linear and rotational motions.
Moment of inertia, radius of gyration, values of moments of inertia for simple geometrical objects (no derivation).
Unit VI: Gravitation
Chapter–8: Gravitation
Kepler’s Laws of Planetary motion, Universal law of gravitation. Acceleration due to gravity and its variation with altitude and depth. Gravitational potential energy and gravitational potential, escape velocity, orbital velocity of a satellite.
Unit VII: Properties of Bulk Matter.
Chapter–9: Mechanical Properties of Solids
Stress-strain relationship, Hooke’s law, Young’s modulus, bulk modulus, shear modulus, Poisson’s ratio and elastic energy
Chapter–10: Mechanical Properties of Fluids
Pressure due to a fluid column; Pascal’s law and its applications (hydraulic lift and hydraulic brakes), effect of gravity on fluid pressure.
Viscosity, Stokes’ law, terminal velocity, streamline and turbulent flow, critical velocity, Bernoulli’s theorem and its applications.
Surface energy and surface tension, angle of contact, excess of pressure across a curved surface, application of surface tension-ideas to drops, bubbles and capillary rise.
Chapter–11: Thermal Properties of Matter
Heat, temperature, thermal expansion; thermal expansion of solids, liquids and gases, anomalous expansion of water; specific heat capacity; Cp, Cv, calorimetry; change of state- latent heat capacity. Heat transfer-conduction, convection and radiation, thermal conductivity, Qualitative idea of blackbody radiation, Wien’s Displacement law and Stefan’s law
Unit VIII: Thermodynamics
Chapter–12: Thermodynamics
Thermal equilibrium and definition of temperature, zeroth law of thermodynamics, heat, work and internal energy. First law of thermodynamics, isothermal and adiabatic processes.
Second law of thermodynamics: reversible and irreversible processes, Cyclic Processes.
Unit IX: Behaviour of Perfect Gases and Kinetic Theory of Gases.
Chapter–13: Kinetic Theory
Equation of state of a perfect gas, work done in compressing a gas.
Kinetic theory of gases – assumptions, concept of pressure. Kinetic interpretation of temperature; rms speed of gas molecules; degrees of freedom, law of equi-partition of energy (statement only) and application to specific heat capacities of gases; concept of mean free path, Avogadro’s number.
Unit X: Oscillations and Waves
Chapter–14: Oscillations
Periodic motion – time period, frequency, displacement as a function of time, periodic functions. Simple harmonic motion (S.H.M) and its equation; phase; oscillations of a loaded spring- restoring force and force constant; energy in S.H.M. Kinetic and potential energies; simple pendulum, derivation of expression for itstime period.
Chapter–15: Waves
Wave motion: Transverse and longitudinal waves, speed of travelling wave,
displacement relation for a progressive wave, principle of superposition of waves,reflection of waves, Standing waves in strings and organ pipes: fundamental mode and harmonics, Beats.
Chemistry (70 Marks)
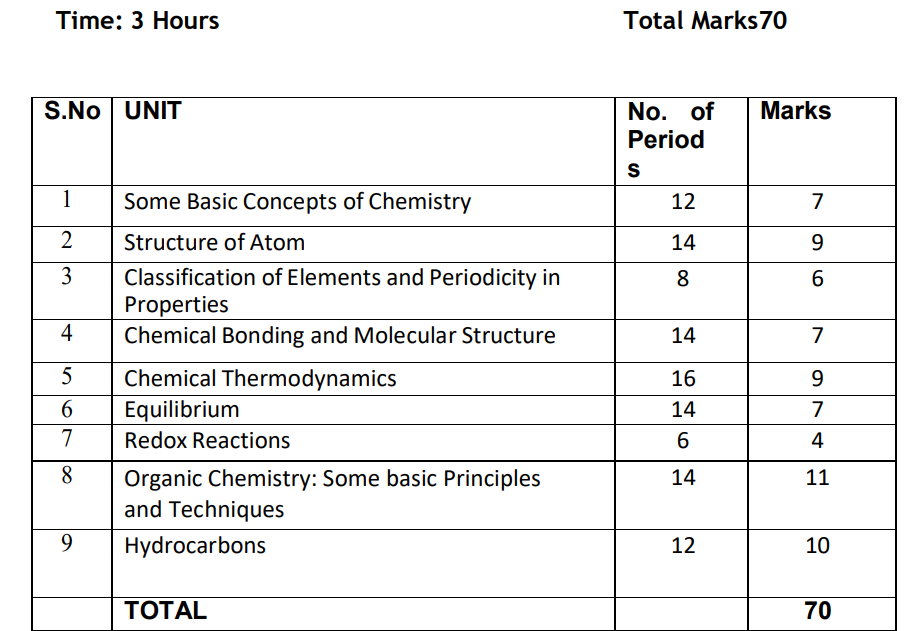
Unit 1: Some Basic Concepts of Chemistry
General Introduction: Importance and scope of Chemistry.
Nature of matter, laws of chemical combination, Dalton’s atomic theory: concept of elements, atoms and molecules.
Atomic and molecular masses, mole concept and molar mass, percentage composition, empirical and molecular formula, chemical reactions, stoichiometry and calculations based on stoichiometry.
Unit 2: Structure of Atom
Discovery of Electron, Proton and Neutron, atomic number, isotopes and isobars. Thomson’s model and its limitations. Rutherford’s model and its limitations, Bohr’s model and its limitations, concept of shells and subshells, dual nature of matter and light, de Broglie’s relationship, Heisenberg uncertainty principle, concept of orbitals, quantum numbers, shapes
of s, p and d orbitals, rules for filling electrons in orbitals – Aufbau principle, Pauli’s exclusion principle and Hund’s rule, electronic configuration of atoms, stability of half-filled and completely filled orbitals.
Unit 3: Classification of Elements and Periodicity in Properties
Significance of classification, brief history of the development of periodic table, modern periodic law and the present form of periodic table, periodic trends in properties of elements -atomic radii, ionic radii, inert gas radii, Ionization enthalpy, electron gain enthalpy, electronegativity,valency. Nomenclature of elements with atomic number greater than 100.
Unit 4: Chemical Bonding and Molecular Structure
Valence electrons, ionic bond, covalent bond, bond parameters, Lewis structure, polar character of covalent bond, covalent character of ionic bond, valence bond theory, resonance, geometry of covalent molecules, VSEPR theory, concept of hybridization, involving s, p and d orbitals and shapes of some simple molecules, molecular orbital theory of homonuclear diatomic
molecules(qualitative idea only), Hydrogen bond.
Unit 5: Chemical Thermodynamics
Concepts of System and types of systems, surroundings, work, heat, energy, extensive and intensive properties, state functions.
First law of thermodynamics -internal energy and enthalpy, heat capacity and specific heat, measurement of U and H, Hess’s law of constant heat summation, enthalpy of bond dissociation, combustion, formation, atomization, sublimation, phase transition, ionization, solution and dilution.
Second law of Thermodynamics(brief introduction)
Introduction of entropy as a state function, Gibb’s energy change for spontaneous and nonspontaneous processes, criteria for equilibrium. Third law of thermodynamics (brief introduction).
Unit 6: Equilibrium
Equilibrium in physical and chemical processes, dynamic nature of equilibrium, law of mass action, equilibrium constant, factors affecting equilibrium – Le Chatelier’s principle, ionic equilibrium- ionization of acids and bases, strong and weak electrolytes, degree of ionization, ionization of poly basic acids, acid strength, concept of pH, hydrolysis of salts (elementary idea), buffer solution, Henderson Equation, solubility product, common ion effect (with illustrative
examples).
Unit 7: Redox Reactions
Concept of oxidation and reduction, redox reactions, oxidation number, balancing redox reactions, in terms of loss and gain of electrons and change in oxidation number, applications of redox reactions.
Unit 8: Organic Chemistry -Some Basic Principles and Techniques
General introduction, methods of purification, qualitative and quantitative analysis, classification and IUPAC nomenclature of organic compounds. Electronic displacements in a covalent bond: inductive effect, electromeric effect, resonance and hyper conjugation. Homolytic and heterolytic fission of a covalent bond: free radicals, carbocations, carbanions, electrophiles and nucleophiles, types of organic reactions.
Classification of Hydrocarbons
Aliphatic Hydrocarbons:
Alkanes – Nomenclature, isomerism, conformation (ethane only), physical properties, chemical reactions including free radical mechanism of halogenation, combustion and pyrolysis. Alkenes – Nomenclature, structure of double bond (ethene), geometrical isomerism, physical properties, methods of preparation, chemical reactions: addition of hydrogen, halogen, water, hydrogen halides (Markovnikov’s addition and peroxide effect), ozonolysis, oxidation, mechanismof electrophilic addition.
Alkynes – Nomenclature, structure of triple bond (ethyne), physical properties, methods of preparation, chemical reactions: acidic character of alkynes, addition reaction of – hydrogen, halogens, hydrogen halides and water.
Aromatic Hydrocarbons:
Introduction, IUPAC nomenclature, benzene: resonance, aromaticity, chemical properties: mechanism of electrophilic substitution. Nitration, sulphonation, halogenation, Friedel Craft’s alkylation and acylation, directive influence of functional group in monosubstituted benzene. Carcinogenicity and toxicity.
Biology (70 Marks)

Unit: I DIVERSITY IN THE LIVING WORLD
Chapter-1 The Living World
Biodiversity: Classification of living organisms, Taxonomy and Systemtics, Taxonomic Categories (From species to kingdom) Biological classification, Binomial nomenclature (Brief idea)
Chapter-2: Biological Classification
Five Kingdom classification, Salient features and classification of Monera, Protista, Fungi into major groups; lichens, viruses, viroid and prions.
Chapter-3: Plant Kingdom
Classification of plants into major groups, salient and distinguishing features and a few examples of Algae, Bryophytes, Pteridophytes, Gymnosperms and preliminary idea of Angiosperms.
Chapter-4: Animal Kingdom
Basis of classification. Salient features and classification of animals, Non-chordates upto phyla level and chordates upto class level (salient features and a few examples of each category) (No live animals or specimens should be displayed)
Unit-II : STRUCTURAL ORGANISATION IN PLANTS AND ANIMALS
Chapter-5 Morphology of flowering Plants
Morphology of different parts of flowering plants- root, stem, leaf, inflorescence, flower, fruit and seed. Description of family solanaceae
Chapter-6 Anatomy of Flowering Plants
Types of tissues; Tissue Systems in dicots and monocots, Anatomy of Dicotyledonous and Monocotyledonous plants.
Chapter-7 Structural Organisation in Animals
Morphology, Anatomy and functions of different systems (Digestive, Circulatory, Respiratory, Nervous and Reproductive) of frog.
Unit-III: CELL: STRUCTURE AND FUNCTION
Chapter-8 Cell: The Unit of Life
Cell theory and cell as the basic unit of life, structure of Prokaryotic and Eukaryotic cells: Plant cell and animal cell: Cell envelope; cell membrane, cell wall. Structure and function of endomembrane system, endoplasmic reticulum, Golgi bodies, lysosomes, vacuoles, mitochondria, ribosomes, plastids, microbodies, cytoskeleton, cilia, flagella, centrosome and centrioles (ultra structure and function): nucleus and its ultrastractures.
Chapter-9 Biomolecules
Chemical constituents of living cells: bionolecules ,structure and functions of Proteins, Carbohydrates and Nucleic Acids. Enzymes-Types, Properties, enzyme action, classification and nomenclature of enzymes.
Chapter-10 : Cell Cycle and Cell Division
Cell Cycle. Mitosis and Meiosis – their phases and their significance.
Unit-IV: PANT PHYSIOLOGY
Chapter -11: Photosynthesis in Higher Plants
Early experiments relating to photosynthesis. Photosynthesis as a means of autotrophic nutrition: Site of photosynthesis ,Pigments involved in photosynthesis(elementary idea ) ,Photochemical and biosynthetic phases of photosynthesis, cyclic and non-cyclic photophosphorylation, chemiosmotic
hypothesis; photorespiration; C3 and C4 pathways, factors affecting photosynthesis.
Chapter -12 Respiration in Plants
Exchange of gases ; Cellular respiration: Glycolysis ,Fermentation ,(anaerobic) ,TCA Cycle and Electron transport system (aerobic ) ,Energy relations – Number of ATP molecules generated ,anphibolic pathway ,respiratory quotient .
Chapter -13 Plant Growth and Development
Phases of Plant Growth and Plant Growth rate ,conditions required for growth ,differentiation, dedifferentiation and redifferentiation. Sequence of developmental process in a plants cell Plant,
Growth regulators-Auxin, Gibberelins, Cytokinins. Eltylene , ABA.
Unit-V: HUMAN PHYSIOLOGY
Chapter-14 Breathing and Exchange of Gases
Respiratory organs in animal (recall only); Respiratory system in humans; mechanism of breathing and its regulation in humans-exchange of gases, transport of gases and regulation of respiration, respiratory volume, disorders related to respiration- Asthma, Emphysema, Occupational respiratory
disorders.
Chapter-15: Body Fluids and Circulation
Composition of blood; blood groups; coagulation of blood; composition of lymph and its function; human circulatory system- structure of human heart and blood vessels; cardiac cycle, cardiac output, ECG; double circulation; regulation of cardiac activity; disorders of circulatory systemhypertension, coronary artery disease, angina pectoris, heart failure.
Chapter-16: Excretory Products and their elimination
Modes of Excretion- ammonotelism, ureotelism, uricotelism; human excretory system-structure and function-urine formation, osmoregulation, regulation of kidney function-renin angiotensin, mechanism, atrial natriuretic factor, ADH and diabetes insipidus; role of other organs in excretion: excretory disorder-uremia, renal failure, renal calculi, nephritis, dialysis and artificial kidney, kidney
transplant.
Chapter-17: Locomotion and Movement
Types of movement-ciliary, flagellar, muscular, skeletal muscle, contractile proteins and mechanism of muscle contraction; skeletal system and its functions; joints, disorders of muscular and skeletal systems- myasthenia gravis, tetany, muscular dystrophy, arthritis, osteoporosis, gout.
Chapter-18: Neural Control and Coordination
Neuron and Nerves; Nervous system in human-Central nervous system; Peripheral nervous system and Visceral nervous system; generation and conduction of nerve inpulse.
Chapter-19: Chemical Coordination and Integration
Endocrine glands and hormones; human endocrine system- Hypothalamus, Pituitary, Pincal, Thyroid, Parathyroid, Adrenal, Pancreas, Gonads. Mechanism of hormone action (elementary idea), role of hormonesas messengers and regulators, hypo and hyperactivity and related disorders, dwarfism, acromegaly, cretinism, goiter, exophthalanic goiter, diabetes, Addison’s disease
Note: (Diseases related to all the human physiological systems to be taught in brief)
Mathematics (100 Marks)
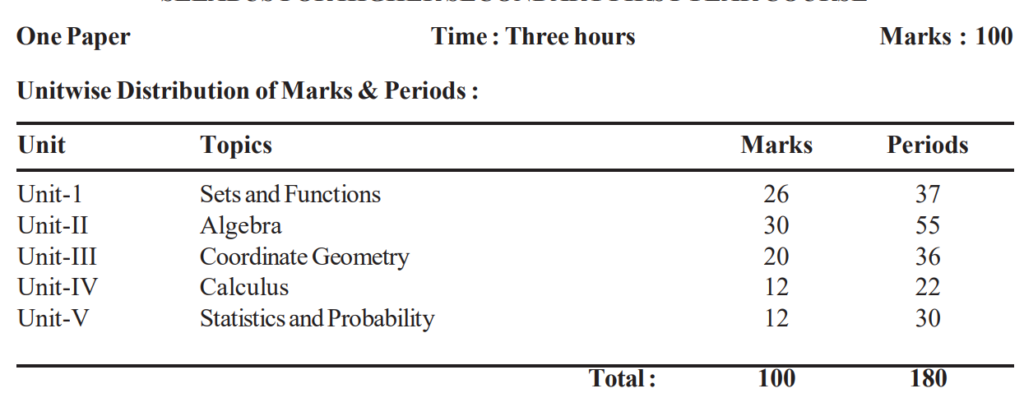
Unit-I : SETS AND FUNCTIONS
1. Sets:
Sets and their representations, Empty set, Finite and Infinite sets, Equal sets, Subsets, Subsets of the set of real numbers especially intervals (with notations), Universal set, Venn diagrams, Union and Intersection of sets, Difference of sets, Complement of a set.
2. Relations and Functions:
Cartesian product of sets, Number of elements in the Cartesian product of two finite sets, Cartesian product of the reals with itself(upto R×R×R).
Definition of relation, pictorial diagrams, domain, co-domain and range of a relation, Function as a special kind of relation from one set to another, Pictorial representation of a function, domain, co-domain and range of a function, Real valued function of the real variable, domain and range of these functions, constant,identity,polynomial,rational,modulus,signumandgreatestintegerfunctions with their graphs, Sum, difference, product and quotients of functions.
3.Trigonometric Functions:
Positive and negative angles, Measuring angle sin radians and in degrees and conversion from one measure to another, Definition of trigonometric functions with the help of unit circle. Truth of the identity sin2x + cos2x = 1, for all x. Sings of trigonometric functions and sketch of their graphs, Expressing sin(x+y) and cos(x+y) interms of sinx, siny, cosx and cosy, Deducing the identities like following: tan(x y) tan x tan y, 1∓ tan x tan y cot(x y)
cot x cot y ∓1, cot y cot x Identities related to sin2x, cos2x, tan2x, sin3x, cos3x and tan3x,
Unit-II : ALGEBRA
1. Complex Numbers and Quadratic Equations:
Need for complex numbers, especially 1 , to be motivated by inability to solve every quadratic equation, Brief description of algebraic properties of complex numbers, The modulus and the conjugate of a complex number. Argand plane and polar representation.
2. Linear Inequalities:
Linear inequalities. Algebraic solutions of linear inequalities in one variable and their representation on the number line.
3. Permutations and Combinations:
Fundamental principle of counting, Factorial n. Permutations and combinations, derivation of formulae and their connections, simple applications.
4. BinomialTheorem :
Statement and proof of the binomial theorem for positive integral indices, Pascal’striangle, simple applications.
5. Sequence and Series :
Sequence and Series. Geometric progression (G.P.), general term of a GP. sum of n terms of a GP., geometric mean(G.M.),relation between A.M. and GM.
Unit-III: COORDINATE GEOMETRY
1. Straight Lines:
Brief recall of 2D from earlier classes. Slope of a line and angle between two lines, Various forms of equations of a line, parallel to axes, point-slope form, slope-intercept form, two-point form, intercept form and General equation of a line, Distance of a point from a line.
2. Conic Sections :
Sections of a cone : Circle, ellipse, parabola, hyperbola, a point, a straight line and pair of intersecting lines as a degenerated case of a conic section, Standard equations and simple properties of parabola, ellipse and hyperbola, Standard equation of a circle.
3.Introduction to Three-dimensional Geometry:
Coordinate axes and coordinate planes in three dimensions, Coordinates of a point, Distance between two points.
Unit-IV : CALCULUS
Limits and -Derivatives
Intuitive idea of limits. Limits of polynomials and rational functions, trigonometric, exponential and logarithmic functions. Definition of derivative relate it to scope of tangent of the curve, derivative of sum, difference, product and quotient of functions. Derivatives of polynomial and trigonometric functions.
Unit-V : STATISTICS AND PROBABILITY
1. Statistics:
Measure of Dispersion, Range, Mean deviation, variance and standard deviation of ungrouped/ grouped data.
2. Probability:
Events, Occurrence of events, ‘not’, ‘and’ ‘or’ events, exhaustive events, mutually exclusive events, Axiomatic (set theoretic) probability, connections with the theories of earlier classes, Probability of an event, probability of ‘not’, ‘and’& ‘or’ events.
Class 12th Syllabus 2023-24 (Science Stream)
Physics (70 Marks)
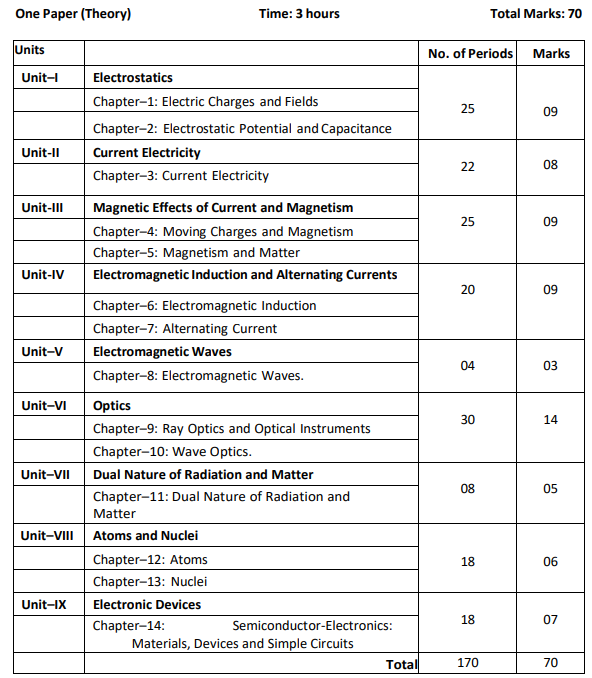
Unit I: Electrostatics
Chapter–1: Electric Charges and Fields
Electric Charges; Conservation of charge, Coulomb’s law-force between two point charges, forces between multiple charges; superposition principle and continuous charge distribution. Electric field, electric field due to a point charge, electric field lines, electric dipole, electric field due to a dipole, torque on a dipole in uniform electric field. Electric flux, statement of Gauss’s theorem
and its applications to find field due to infinitely long straight wire, uniformly charged infinite plane sheet and uniformly charged thin spherical shell (inside and outside).
Chapter–2: Electrostatic Potential and Capacitance
Electric potential, potential difference, electric potential due to a point charge,a dipole and system of charges; equipotential surfaces, electrical potential energy of a system of two-point charges and of electric dipole in an electrostatic field. Conductors and insulators, free charges and bound charges
inside a conductor. Dielectrics and electric polarization, capacitors and capacitance, combination of capacitors in series and in parallel, capacitance of a parallel plate capacitor with and without dielectric medium between the plates, energy stored in a capacitor.
Unit II: Current Electricity
Chapter–3: Current Electricity
Electric current, flow of electric charges in a metallic conductor, drift velocity, mobility and their relation with electric current; Ohm’s law, electrical resistance, combination of resistance(series and parallel) V-I characteristics (linear and non- linear), electrical energy and power, electrical resistivity and conductivity, temperature dependence of resistance. Internal resistance of a cell, potential
difference and emf of a cell, combination of cells in series and in parallel, Kirchhoff’s laws and simple applications, Wheatstone bridge.
Unit III: Magnetic Effects of Current and Magnetism
Chapter–4: Moving Charges and Magnetism
Concept of magnetic field, Oersted’s experiment. Biot – Savart law and its application to current carrying circular loop. Ampere’s law and its applications to infinitely long straight wire. Straight solenoids (only qualitative treatment), force on a moving charge in uniform magnetic and electric fields. Force on a current-carrying conductor in a uniform magnetic field, force between two parallel current-carrying conductors-definition of ampere, torque experienced by a current loop in uniform magnetic field; Current loop as a magnetic dipole and its magnetic dipole moment, moving coil galvanometer-its current sensitivity and conversion to ammeter and voltmeter
Chapter–5: Magnetism and Matter
Bar magnet, bar magnet as an equivalent solenoid (qualitative treatment only). Magnetic field intensity due to a magnetic dipole (bar magnet) along its axis and perpendicular to its axis (qualitative treatment only), torque on a magnetic dipole (bar magnet) in a uniform magnetic field (qualitative treatment only), magnetic field lines. Magnetic properties of materials-Para-, dia-and ferro-magnetic substances with examples, Magnetization of material.
Unit IV: Electromagnetic Induction and Alternating Currents
Chapter–6: Electromagnetic Induction
Electromagnetic induction; Faraday’s laws, induced EMF and current; Lenz’s Law, Self and mutual induction.
Chapter–7: Alternating Current
Alternating currents, peak and RMS value of alternating current/voltage; reactance and impedance; LCR series circuit (Phasor treatment only)resonance; power in AC circuits. AC generator and transformer. Power factor, Wattles current.
Unit V: Electromagnetic waves.
Chapter–8: Electromagnetic Waves
Basic idea of displacement current, Electromagnetic waves, their characteristics, their Transverse nature (qualitative ideas only). Electromagnetic spectrum (radio waves, microwaves, infrared, visible, ultraviolet, X-rays, gamma rays) including elementary facts about their uses.
Unit VI: Optics
Chapter–9: Ray Optics and Optical Instruments
Ray Optics: Reflection of light, spherical mirror and mirror formula Refraction of light, total
internal reflection and its applications, optical fibers, refraction at spherical surfaces, lenses, thin
lens formula, Lens maker’s formula, magnification, power of a lens, combination of thin lenses in
contact, refraction of light through a prism.
Optical instruments: Microscopes and astronomical telescopes (reflecting and refracting) and
their magnifying powers
Chapter–10: Wave Optics
Wave Optics : Wave front and Huygen’s principle, reflection and refraction of plane wave at a plane surface using wave fronts. Proof of laws of reflection and refraction using Huygen’s principle. Interference, Young’s double slit experiment and expression for fringe width, (no derivation, final expression only) coherent sources and sustained interference of light, diffraction due to a single slit, width of central maximum (qualitative treatment only)
Unit VII: Dual Nature of Radiation and Matter.
Chapter–11: Dual Nature of Radiation and Matter
Dual nature of radiation, Photoelectric effect, Hertz and Lenard’s observations; Einstein’s photoelectric equation-particle nature of light. Experimental study of photoelectric effect. Matter waves-wave nature of particles, de-Broglie relation.
Unit VIII: Atoms and Nuclei
Chapter–12: Atoms
Alpha-particle scattering experiment; Rutherford’s model of atom; Bohr model, Bohr’s model of hydrogen atom. Expression of radius of nth orbit, velocity and energy of electron, hydrogen spectra (qualitative treatment only)
Chapter–13: Nuclei
Composition and size of nucleus, Nuclear force, Mass- energy relation, mass defect, binding energy per nucleon and its variation with mass number, nuclear fission, nuclear fusion.
Unit IX: Electronic Devices.
Chapter–14: Semiconductor Electronics: Materials, Devices and Simple Circuits
Energy bands in conductors, semiconductors and insulators (qualitative ideas only) Intrinsic and extrinsic semiconductors, p and n type, p-n junction. Semiconductor diode, I-V characteristics in forward and reverse bias, application of junction diode: diode as a rectifier.
Chemistry (70 Marks)
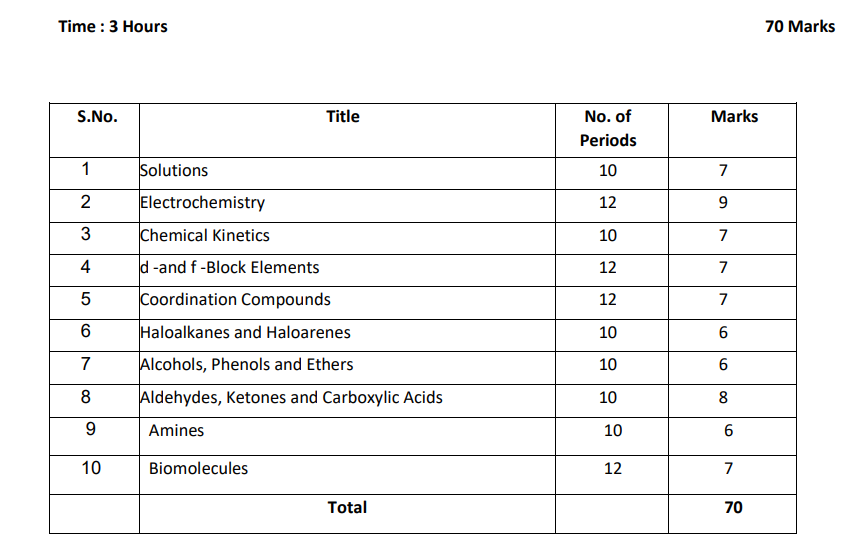
Unit 1: Solutions
Types of solutions, expression of concentration of solutions of solids in liquids, solubility of gases in liquids, solid solutions, Raoult’s law, colligative properties – relative lowering of vapour pressure, elevation of boiling point, depression of freezing point, osmotic pressure, determination of molecular masses using colligative properties, abnormal molecular mass, Van’t Hoff factor.
Unit 2: Electrochemistry
Redox reactions, EMF of a cell, standard electrode potential, Nernst equation and its application to chemical cells, Relation between Gibbs energy change and EMF of a cell, conductance in electrolytic solutions, specific and molar conductivity, variations of conductivity with concentration, Kohlrausch’s
Law, electrolysis and law of electrolysis (elementary idea), dry cell-electrolytic cells and Galvanic cells, lead accumulator, fuel cells, corrosion.
Unit 3: Chemical Kinetics
Rate of a reaction (Average and instantaneous), factors affecting rate of reaction: concentration, temperature, catalyst; order and molecularity of a reaction, rate law and specific rate constant, integrated rate equations and half-life (only for zero and first order reactions), concept of collision theory (elementary idea, no mathematical treatment), activation energy, Arrhenius equation.
Unit 4: d and f Block Elements
General introduction, electronic configuration, occurrence and characteristics of transition metals, general trends in properties of the first row transition metals – metallic character, ionization enthalpy, oxidation states, ionic radii, colour, catalytic property, magnetic properties, interstitial compounds, alloy formation, preparation and properties of K2Cr2O7 and KMnO4.
Lanthanoids – Electronic configuration, oxidation states, chemical reactivity and lanthanoid contraction and its consequences.
Unit 5: Coordination Compounds
Coordination compounds – Introduction, ligands, coordination number, colour, magnetic properties and shapes, IUPAC nomenclature of mononuclear coordination compounds. Bonding, Werner’s theory, VBT, and CFT; structure and stereoisomerism, importance of coordination compounds (in qualitative analysis, extraction of metals and biological system).
Unit 6: Haloalkanes and Haloarenes
Haloalkanes: Nomenclature, nature of C–X bond, physical and chemical properties, optical rotation mechanism of substitution reactions.
Haloarenes: Nature of C–X bond, substitution reactions (Directive influence of halogen in monosubstituted compounds only).
Uses and environmental effects of dichloromethane, trichloromethane, tetrachloromethane, iodoform, freons, DDT.
Unit 7: Alcohols, Phenols and Ethers
Alcohols: Nomenclature, methods of preparation, physical and chemical properties (of primary
alcohols only), identification of primary, secondary and tertiary alcohols, mechanism of dehydration, uses with special reference to methanol and ethanol.
Phenols: Nomenclature, methods of preparation, physical and chemical properties, acidic nature of phenol, electrophillic substitution reactions, uses of phenols.
Ethers: Nomenclature, methods of preparation, physical and chemical properties, uses.
Unit 8: Aldehydes, Ketones and Carboxylic Acids
Aldehydes and Ketones: Nomenclature, nature of carbonyl group, methods of preparation, physical and chemical properties, mechanism of nucleophilic addition, reactivity of alpha hydrogen in aldehydes, uses.
Carboxylic Acids: Nomenclature, acidic nature, methods of preparation, physical and chemical properties; uses.
Unit 9: Amines
Amines: Nomenclature, classification, structure, methods of preparation, physical and chemical properties, uses, identification of primary, secondary and tertiary amines.
Diazonium salts: Preparation, chemical reactions and importance in synthetic organic chemistry.
Unit 10: Biomolecules
Carbohydrates – Classification (aldoses and ketoses), monosaccahrides (glucose and fructose), D-L configuration oligosaccharides (sucrose, lactose, maltose), polysaccharides (starch, cellulose, glycogen); Importance of carbohydrates.
Proteins – Elementary idea of – amino acids, peptide bond, polypeptides, proteins, structure of proteins – primary, secondary, tertiary structure and quaternary structures (qualitative idea only), denaturation of proteins; enzymes. Hormones – Elementary idea excluding structure.
Vitamins – Classification and functions.
Nucleic Acids: DNA and RNA
Biology (70 Marks)
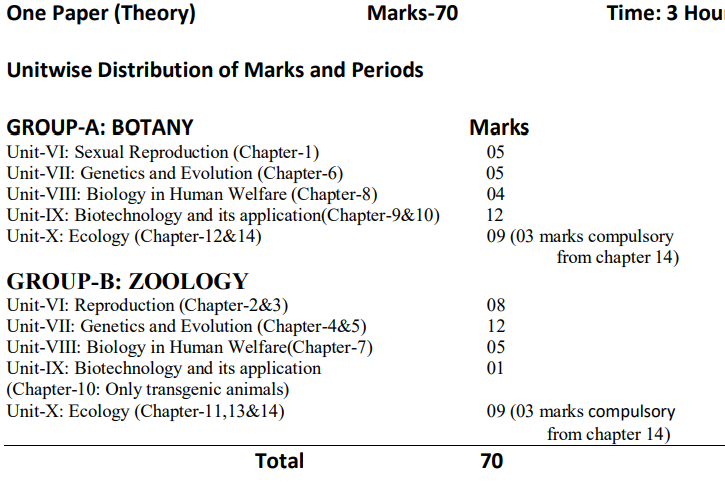
Unit-VI: Reproduction :
Chapter 1 : Sexual Reproduction in Flowering Plants:
(i) Flower-An organ of sexual reproduction of Angiosperms;
(ii)Pre-fertilization: Structures and Events;
(iii)Double Fertilization;
(iv)Post-fertilization: Structures and Events;
(v)Apomisix and Polyembryony.
Chapter 2 : Human reproduction :
(i) The Male Reproductive System;
(ii) The Female Reproductive System;
(iii) Gametogenesis;
(iv) Menstrual Cycle;
(v) Fertilization and Implantation;
(vi) Pregnancy and Embryonic Development;
(vii)Parturition and Lactation.
Chapter 3 : Reproductive Health :
(i) Reproductive Health-Problems and Strategies;
(ii) Population Stabilization and Birth Control;
(iii) Medical Termination of Pregnancy;
(iv) Sexually Transmitted infection;(v)Infertility and Assisted Reproductive Technology
Unit-VII: Genetics and Evolution
Chapter 4 : Principles of Inheritance and Variation:
(i) Mendel’s Laws of Inheritance;
(ii)Inheritance of One Gene;
(iii) Inheritance of Two Genes; Chromosomal Theory of Inheritance; Linkage and recombination
(iv) Sex Determination;
(v)Mutation;
(vi)Genetic Disorders.
Chapter 5 : Molecular Basis of Inheritance :
(i) The DNA;
(ii) The Search for Genetic Material;
(iii) RNA World;
(iv)Replication;
(v)Transcription;
(vi)Genetic Code;
(vii)Translation;
(viii)Regulation of Gene Expression;
(ix)Human Genome Project;
(x)DNA Fingerprinting.
Chapter 6 : Evolution :
(i) Origin of Life;
(ii) Evolution of Life Formes- A Theory;
(iii)Evidences for Evolution;
(iv)Adaptive Radiation;
(v)Biological Evolution;
(vi)Mechanism of Evolution;
(vii)Hardy Weinberg Principle;
(viii)A brief account of Evolution;
(ix)Origin and Evolution of Man.
Unit-VIII: Biologyin Human Welfare
Chapter 7 : Human Health and Diseases:
(i)Common Diseases in Humans; Typhoid, Pneumonia, Common Cold, Malaria, Amaebiasis, Ascariasis, Elephantiasis, Ringworm
(ii)Immunity;
(iii)AIDS;
(vi)Cancer;
(v)Drugs and Alcohol Abuse.
Chapter 8: Microbes in Human Welfare :
(i) Microbes in Household Products;
(ii) Microbes in Industrial Products;
(iii) Microbes in Sewage Treatment;
(iv) Microbes in Production of Biogas;
(v) Microbes as Bio-control Agents;
(vi) Microbes as Bio-fertilisers.
Unit-IX :Biotechnology
Chapter 9 : Biotechnology; Principles and Processes:
(i) Principles of Biotechnology;
(ii)Tools of recombinant DNA Technology;
(iii) Processes of Recombinant DNA Technology.
Chapter 10: Biotechnology and its Application :
(i)Bio-technological Applications in Agriculture;
(ii)Bio-technological Applications in Medicine;
(iii) Transgenic Animals; (iv)Ethical Issues.
Unit-X : Ecology
Chapter 11 :Organisms and Populations:
(i) Organism and its Environment;
(ii) Populations- Population Attributes; Population Growth and Population Interactions.
Chapter 12 :Ecosystems:
(i)Ecosystem- Structure and Function;
(ii) Productivity;
(iii) Decomposition;
(iv) Energy Flow;
(v)Ecological Pyramids;
Chapter 13 :Biodiversity and Conservation:
(i)Biodiversity;
(ii)Biodiversity Conservation;
(iii)National Park and Sanctuaries of Assam with special reference to conservation of endangered species.
Chapter 14 : Bioresources of Assam :
(i) Medicinal (Sarpagandha, Neem, Tulsi, Cinchona and Atropa) Timber Yielding (Teak, Sal, Sissoo, Gomari, Hollong) Plants;
(ii) Sericogenic Re-sources (Muga andEri)
Mathematics (100 Marks)

Unit-I: 1. RELATIONS AND FUNCTIONS
Types of relations: Reflexive, symmetric, transitive and equivalence relations. Types of function, composition of functions and invertible function.
2. Inverse Trigonometric Functions :Definition, range, domain, principal value branches. Graphs of inverse trigonometric functions. Elementary properties of inverse trigonometric functions.
Unit-II: ALGEBRA
1. Matrices:
Concept, notation, order, equality, types of matrices, zero matrix, transpose of a matrix, symmetric and skew symmetric matrices. Addition, multiplication and scalar multiplication of matrices, simple properties of addition, multiplication and scalar multiplication. Non-commutativity of multiplication of matrices
and existence of non-zero matrices whose product is the zero matrix (restrict to square matrices of order 2). Invertible matrices, proof of uniqueness of inverse if it exist.
2. Determinants : Determinant of a square matrix (up to 3 × 3 matrices), properties of determinants, minors, cofactors and applications of determinants in finding the area of a triangle. Adjoint and inverse of a square matrix.
Consistency, inconsistency and number of solutions of system of linear equations by example, solving system of linear equations in two or three variables (having unique solution) using inverse of a matrix.
Unit-III: CALCULUS
1. Continuity and Differentiability :
Continuity and differentiability, derivative of composite functions, chain rule, derivatives of inverse trigonometric functions, derivative of implicit function. Concept of exponential and logarithmic functions and their derivatives. Logarithmic differentiation. Derivative of functions expressed in parametric forms. Second order derivatives
2. Application of Derivatives :
Applications of derivatives : Rate of change, increasing/ decreasing functions, maxima and minima (first derivative test motivated geometrically and second derivative test given as a provable tool). Simple problems(that illustrate basic principles and understanding of the subject as well as real-life situations)
3. Integrals :
Integration as inverse process of differentiation. Integration of a variety of functions by substitution, by partial fractions and by parts, Evaluation of integrals of the type.
Fundamental Theorem of Calculus (without proof). Basic properties of definite integrals and evaluation of definite integrals.
4. Applications of the Integrals : Applications in finding the area under simple curves, especially lines, arcs of circles/ parabolas/ ellipses (in standard form only),
5. Differential Equations : Definition, order and degree, general and particular solutions of a differential equation. Solution of
differential equations by method of separation of variables, solution of homogeneous differential
equations of first order and first degree. Solutions of linear differential equation of the type :
where P and Q are functions of x.
Unit-IV: VECTORS AND THREE-DIMENSIONAL GEOMETRY
1. Vectors:
Vectors and scalars, magnitude and direction of a vector. Direction cosines/ratios of vectors. Types of vectors(equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Scalar(dot) product of vectors, projection of a vector on a line. Vector (cross) product of vectors.
2. Three-dimensional Geometry :
Direction cosines and direction ratios of a line joining two points. Cartesian and vector equation of a line, Angle between two lines, skew lines, shortest distance between two lines.
Unit-V : LINEAR PROGRAMMING
Introduction, related terminology such as constraints, objective function, optimization, graphical method of solution for problems in two variables, feasible and infeasible regions (bounded or unbounded), feasible and infeasible solution, optimal feasible solution.
Unit-VI: PROBABILITY
Multiplication theorem on probability. Conditional probability, independent events, total probability, Baye’s theorem. Random variable and it’s probability distribution.
Latest Article
NEET UG 2024 Final Revised Result- Announced
Discover the latest updates on the NEET UG 2024 final...
Read MoreNEET 2024 Scam- Supreme Court Hearing
NEET UG 2024 scam, Supreme Court directives, and what it...
Read MoreAssam NEET 2024 Cut-off For MBBS Seats
Discover the expected Assam NEET 2024 cut-off for MBBS seats,...
Read MoreJEE Main Cutoff 2024 Released: Understanding the Implications
The JEE Main Cutoff 2024 has been released. Discover the...
Read More
